# WIKIWIKI 告诉我 —— 何为并查集
在计算机科学中,并查集(Union-Find)是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。 并查集存在两个操作(1.union 联合 2.find 查找) 和一个需要解答的问题(1.isConnected 或 isSameSet 是否是相互连接,或者说是否在同一个集中)
# 思考几个问题
- wiki 告诉我们并查集这种数据结构可以解决一个问题(可以考察两个节点是否相通),那么并查集可以解决那些实际问题呢?
- 我们实现并查集这种数据结构需要几个步骤呢(union、find、isConnected…)?
# 实现
我们这里直接采用基于 Rank 合并(合并时将元素所在深度小的集合合并到元素所在深度大的集合)方式的实现。
# 我们还是先看图
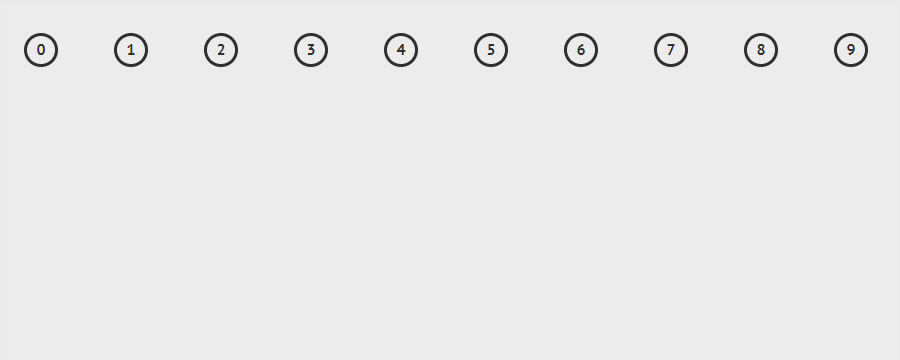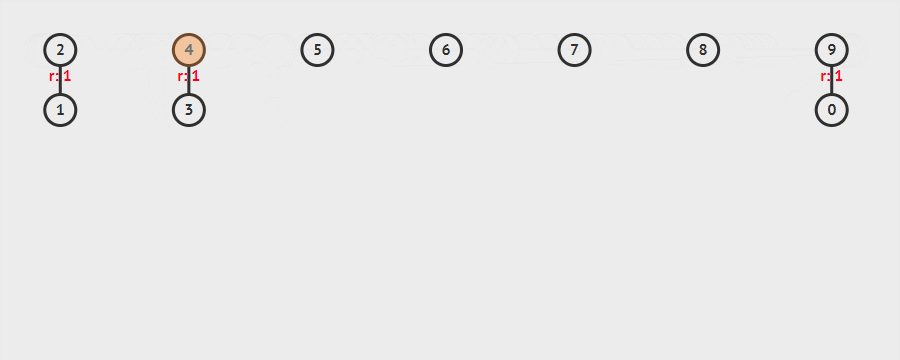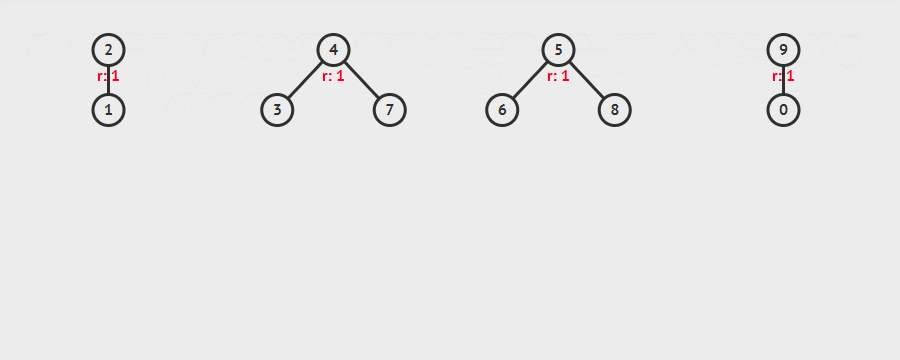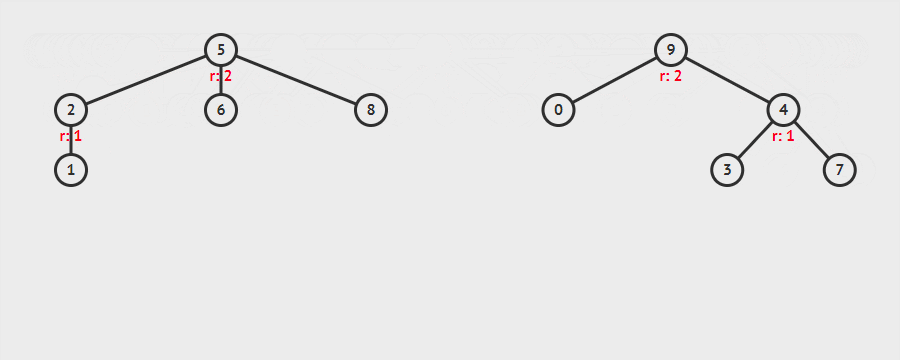
我们在这儿可以回答一下上面提出的第二个问题,实现并查集所需要的几个步骤:
- 初始化元素
- 实现元素与元素间的联合操作
- 实现查找元素所在树的根节点
- 解决一个问题,判定两个元素是否在同一棵树上(两个元素是否相互连接)
# 再来看代码
public class UnionFind {
private int[] parent; // 标注当前元素的父节点的位置
private int[] rank; // 标注当前元素的层级数
private int size; // 并查集中的元素个数
public UnionFind (int size){
this.size = size;
parent = new int[size];
rank = new int[size];
init();
}
private void init() {
for (int i = 0; i < size; i++) {
// 初始化时所有的节点的父节点指向本身,所有的元素层级均为 1
parent[i] = i;
rank[i] = 1;
}
}
/**
* 寻找当前节点的根节点元素
* @param target
* @return
*/
public int find(int target) {
if(target >= size)
throw new ArrayIndexOutOfBoundsException();
if(target == parent[target])
return target;
return find(parent[target]);
}
/**
* 连接两个元素
* @param p
* @param q
*/
public void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot)
return;
if(rank[pRoot] > rank[qRoot]) { // p 所在的树的高度比 q 所在输的高度高,这时应该让 q 的根节点元素连接到 p 的根节点元素
parent[qRoot] = pRoot; // 此时树的高度不变
} else if(rank[pRoot] < rank[qRoot]) {
parent[pRoot] = qRoot; // 此时树的高度不变
} else {
parent[pRoot] = qRoot; // 此时树的高度 +1
rank[qRoot] += 1;
}
}
/**
* 判断两个节点是否连接
* @param p
* @param q
* @return
*/
public boolean isConnected(int p, int q) {
// 如果两个节点的根节点一致则表示这两个节点是相连接的
return find(p) == find(q);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
测试类:
public static void main(String[] args) {
int size = 10;
// Step 1: init()
UnionFind uf = new UnionFind(size);
// Step 2: union()
uf.union(1,2);
uf.union(3,4);
uf.union(0,9);
uf.union(4,7);
uf.union(6,5);
uf.union(5,8);
uf.union(3,9);
uf.union(1,8);
// Step 3: find()
System.out.println(uf.find(0)); // 9
System.out.println(uf.find(1)); // 5
System.out.println(uf.find(2)); // 5
System.out.println(uf.find(3)); // 9
System.out.println(uf.find(4)); // 9
System.out.println(uf.find(5)); // 5
System.out.println(uf.find(6)); // 5
System.out.println(uf.find(7)); // 9
System.out.println(uf.find(8)); // 5
System.out.println(uf.find(9)); // 9
// Step 4: isConnected
System.out.println(uf.isConnected(0,1)); // false
System.out.println(uf.isConnected(1,2)); // true
System.out.println(uf.isConnected(3,4)); // true
System.out.println(uf.isConnected(5,6)); // true
System.out.println(uf.isConnected(7,8)); // false
System.out.println(uf.isConnected(8,9)); // false
System.out.println(uf.isConnected(2,4)); // false
System.out.println(uf.isConnected(3,5)); // false
System.out.println(uf.isConnected(5,6)); // true
System.out.println(uf.isConnected(7,9)); // true
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
我们可以分解这几歩操作
# Step 1: init()

# Step 2: union()
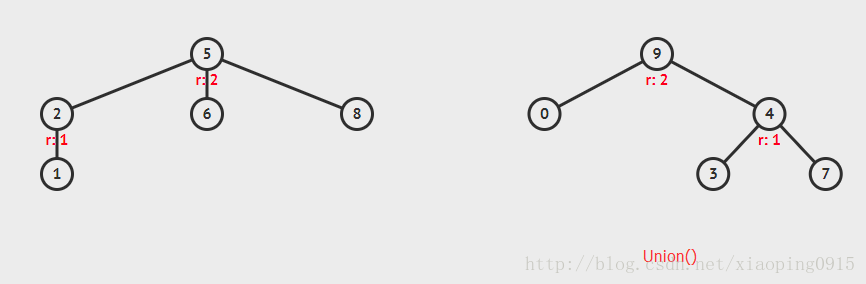
# Step 3: find()
if(target == parent[target])
return target;
return find(parent[target]);
1
2
3
2
3
递归去寻找目标的父亲节点,直到寻找到根节点为止
# Step 4: isConnected()
return find(p) == find(q);
1
考察两个节点的根节点是否是同一个,即考察两个节点是否在同一棵树上。
# 更多关于并查集
并查集(Union-Find)算法介绍 (opens new window)
Gif Power By https://visualgo.net (opens new window)