简介

关于堆排序（HeapSort），堆这种数据结构比这种排序算法更为有价值。

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆，是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值，即A[PARENT[i]] >= A[i]。在数组的非降序排序中，需要使用的就是大根堆，因为根据大根堆的要求可知，最大的值一定在堆顶。(from 百度百科)

这里需要补充介绍一下堆这种数据结构：

堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：

1. 堆中某个节点的值总是不大于或不小于其父节点的值；
2. 堆总是一棵完全二叉树。

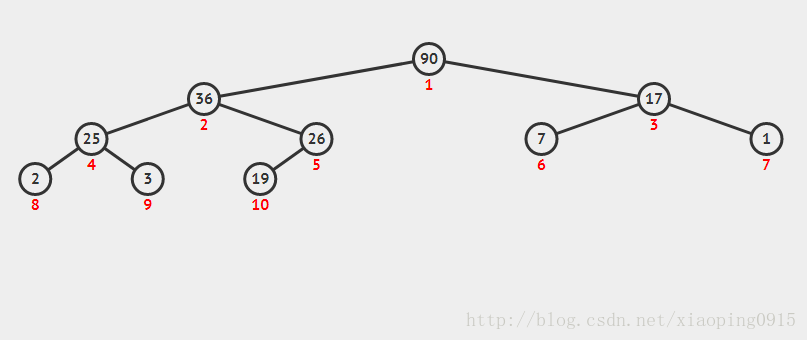
我们可以根据性质一的描述将堆分为最大堆（子节点永远小于父节点）、最小堆（子节点永远大于父节点），上图所示是一个最大堆。我们可以在计算机中使用一个数组来存储一个堆。

[ -, 90, 36, 17, 25, 26, 7, 1, 2, 3, 10 ]

注意我们将数组下标为 0 的位置弃用了，根据图示我们不难得出一个节点的父节点和子节点的下标位置。

1. 父节点的位置： i/2
2. 左子节点的位置： i*2
3. 右子节点的位置： i*2 + 1

维护堆

维护一个堆需要做两件事情：进队和出队

进队

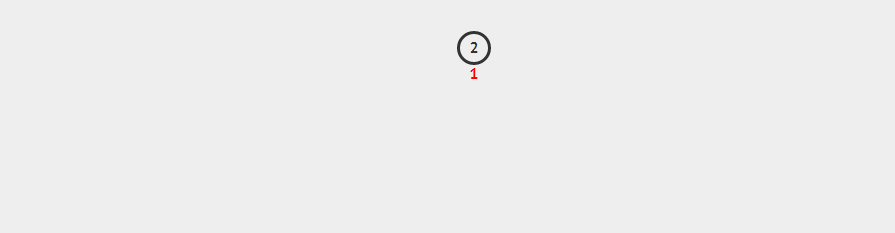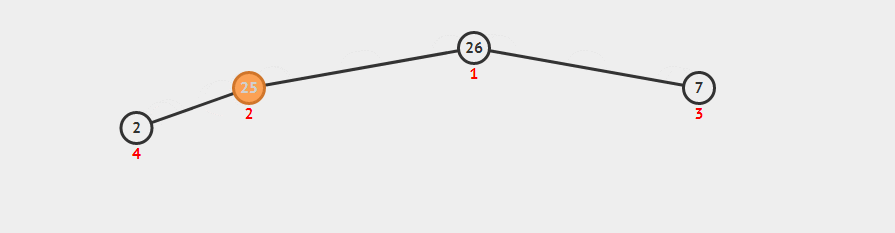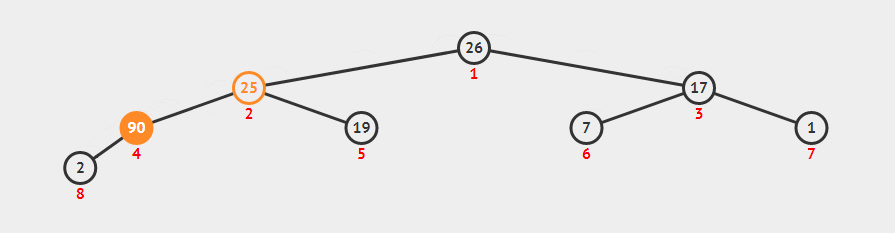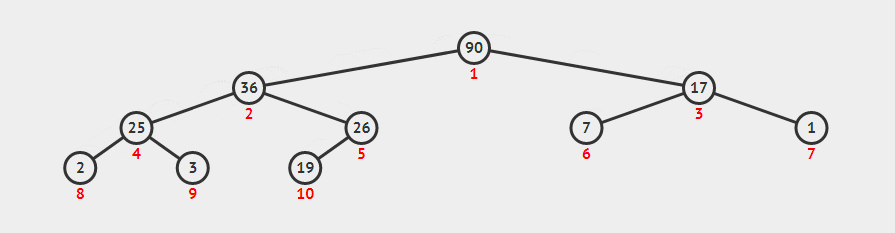
进队需要做的事情很简单，先将元素丢进队列尾，然后和父节点进行比较，比父节点大时则于其交换位置，比父节点小时则表示进队完成。

出队

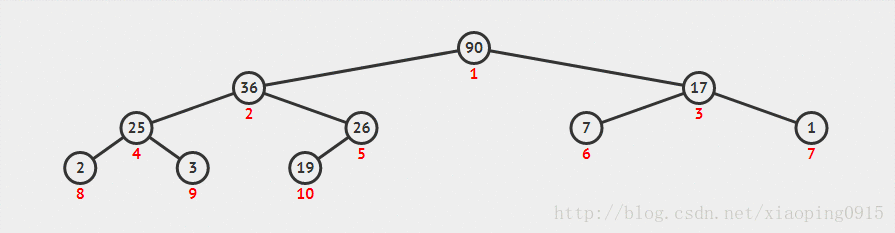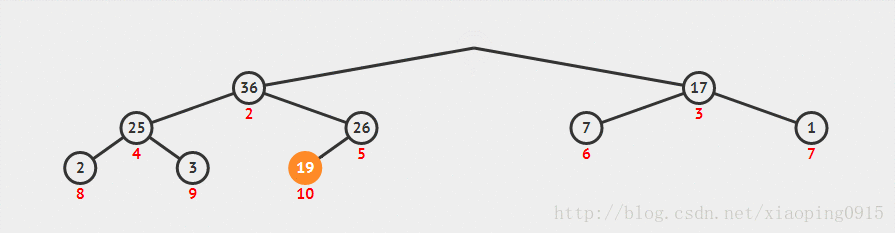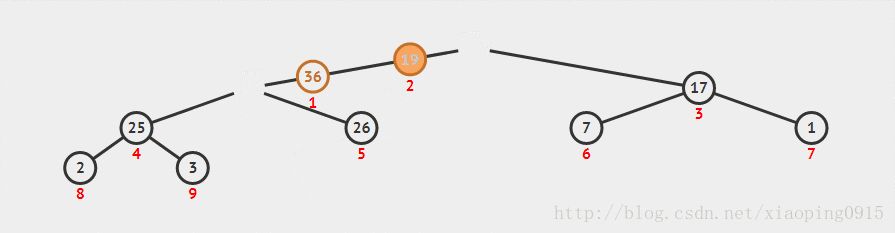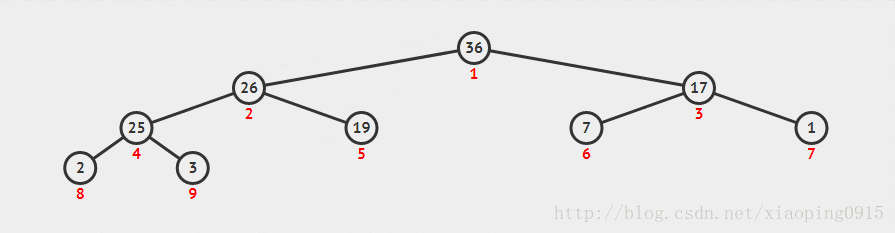
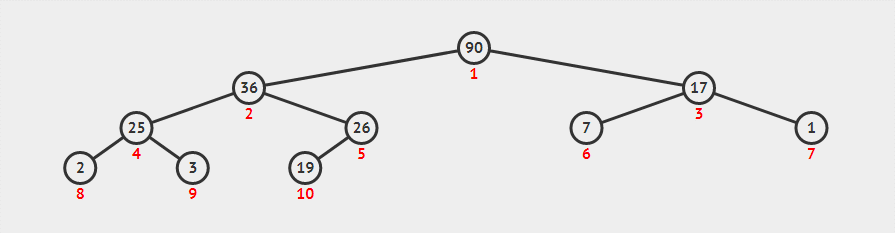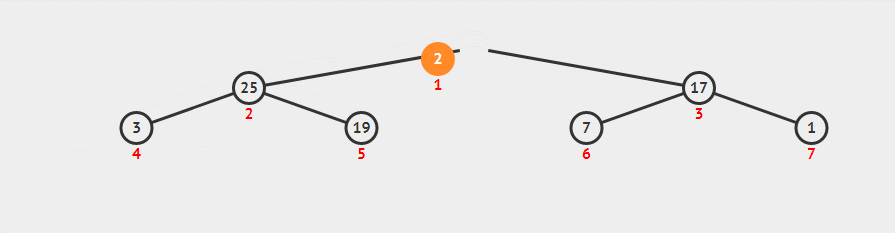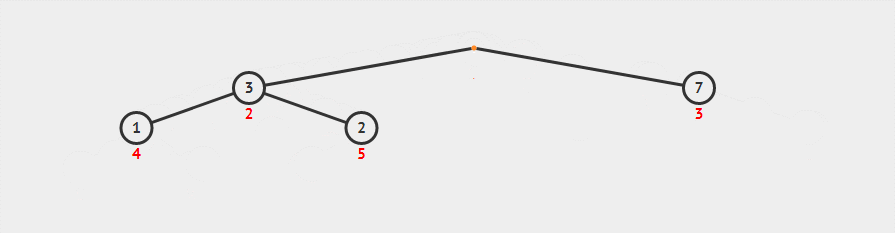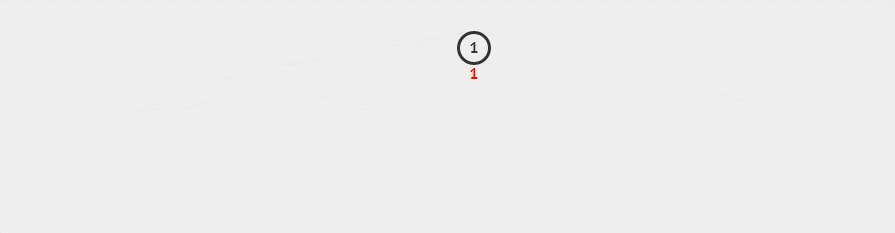
出队像上图所示，也非常简单，只需要将队列头位置的元素取出（下标为 1 的元素），然后将队列尾的元素填充到队列头，接下来和子节点较大者对换位置，直至比子节点的元素都要大时结束交换位置。

排序

在弄清楚了堆的维护之后我们只需要将数组中的元素入队和出队，即可完成整个排序过程。

Java 实现

MaxHeap.java

/**
 * 最大二叉堆
 * 概念： 父结点的键值总是大于或等于任何一个子节点的键值
 */
public class MaxHeap {
    // 模拟最大堆的数组，记录从 1 开始

    private int[] heapArr;

    // 当前位置的计数，由此可得出：
    // 父节点位置 count/2 ；
    // 左边的子节点 count * 2 ；
    // 右边的子节点 count * 2 + 1 。
    private int count;

    // 堆的大小
    private int length;

    /**
     * @param length 申明 heapArr 的长度
     */
    public MaxHeap(int length) {
        this.heapArr = new int[length + 1];
        this.count = 0;
        this.length = length;
    }

    public int size() {
        return count;
    }

    public boolean isEmpty() {
        return count == 0;
    }

    /**
     * 插入一个新的元素
     * @param item
     */
    public void insert(int item) {
        if(count + 1 > length) throw new ArrayIndexOutOfBoundsException();
        heapArr[count + 1] = item;
        count ++;
        shiftUp(count);
    }

    /**
     * 取出最大（优先）的元素
     * @return 存在即取出改元素，若不存在则返回 Integer 最小值
     */
    public int extractMax() {
        if(count < 1) throw new ArrayIndexOutOfBoundsException();
        int ret = heapArr[1];
        swap(heapArr, 1, count );
        count --;
        shiftDown(1);
        // 由于上面的 count-- 了，即 count >= 0 表明下标为 1 的位置存在值
        return count >= 0?ret:Integer.MIN_VALUE;
    }

    /**
     * 将堆中最大的元素出队，并调整最大二叉堆的位置，保持最大二叉堆的定义
     */
    private void shiftDown(int n) {
        while (n*2 <= count) { // 当 n 位置的元素存在子节点时
           // 较出左节点和右节点的较大的元素，然后将较大元素与 n 位置元素比较，若 n 位置元素较小则与其交换位置
            int j = n*2; // 较大子节点下标，初始化为左子节点
            if(j + 1 <= count) { // 存在右节点
                j = heapArr[j + 1] > heapArr[j]?j+1:j;
            }
            if(heapArr[n] < heapArr[j]) {
                swap(heapArr, n, j);
                n = j;
            }else {
                break;
            }
        }
    }

    /**
     * 调整位置为 n 的元素的位置，即保持最大二叉堆的定义 -> 父结点的键值总是大于或等于任何一个子节点的键值
     * @param n 需要调整的元素的位置
     */
    private void shiftUp(int n) {
        while (n > 1 && heapArr[n/2] < heapArr[n]) {
            swap(heapArr, n/2, n);
            n = n/2;
        }
    }

    /**
     * 交换数组中的两个元素
     * @param arr
     * @param a
     * @param b
     */
    private void swap(int[] arr,int a,int b){
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }

}

测试方法

    public static void main(String[] args) {
        MaxHeap maxHeap = new MaxHeap(100);
        int [] testArr = {2,7,26,25,19,17,1,90,3,36};
        for (int i = 0; i < testArr.length; i++) {
            maxHeap.insert(testArr[i]);
        }

        for (int i = 0; i < testArr.length; i++){
            System.out.print( maxHeap.extractMax() );
            if(i != testArr.length - 1) System.out.print(", ");
        }

    }

堆排序的过程

最后

过两天就新年了，祝愿各位朋友新年快乐！

还有需要一提的是： 该算法存在优化的途径，比如说在入队时可以采取直接整个数组入队的方式；以及在交换方式上优化，使用赋值的方式取代（直接算出需要交换的值，避免多次交换值），诸君加油。

Gif Power By https://visualgo.net (opens new window)